Die einfache harmonische Bewegung wurde 1822 vom französischen Mathematiker Baron Jean Baptiste Joseph Fourier erfunden. Edwin Armstrong (18. Dezember 1890 bis 1. Februar 1954) beobachtete 1992 in ihren Experimenten Schwingungen und Alexander Meissner (14. September 1883 bis 3. Januar 1958) erfand Oszillatoren im März 1993. Der Begriff harmonisch ist ein lateinisches Wort. Dieser Artikel beschreibt einen Überblick über den harmonischen Oszillator, einschließlich seiner Definition, seines Typs und seiner Anwendungen.
Was ist ein harmonischer Oszillator?
Der harmonische Oszillator ist definiert als eine Bewegung, bei der die Kraft vom Gleichgewichtspunkt direkt proportional zum Teilchen ist und eine Ausgabe in einer sinusförmigen Wellenform erzeugt. Die Kraft, die Harmonische verursacht Bewegung kann mathematisch ausgedrückt werden als
F = -Kx
Wo,
F = Kraft wiederherstellen
K = Federkonstante
X = Abstand vom Gleichgewicht

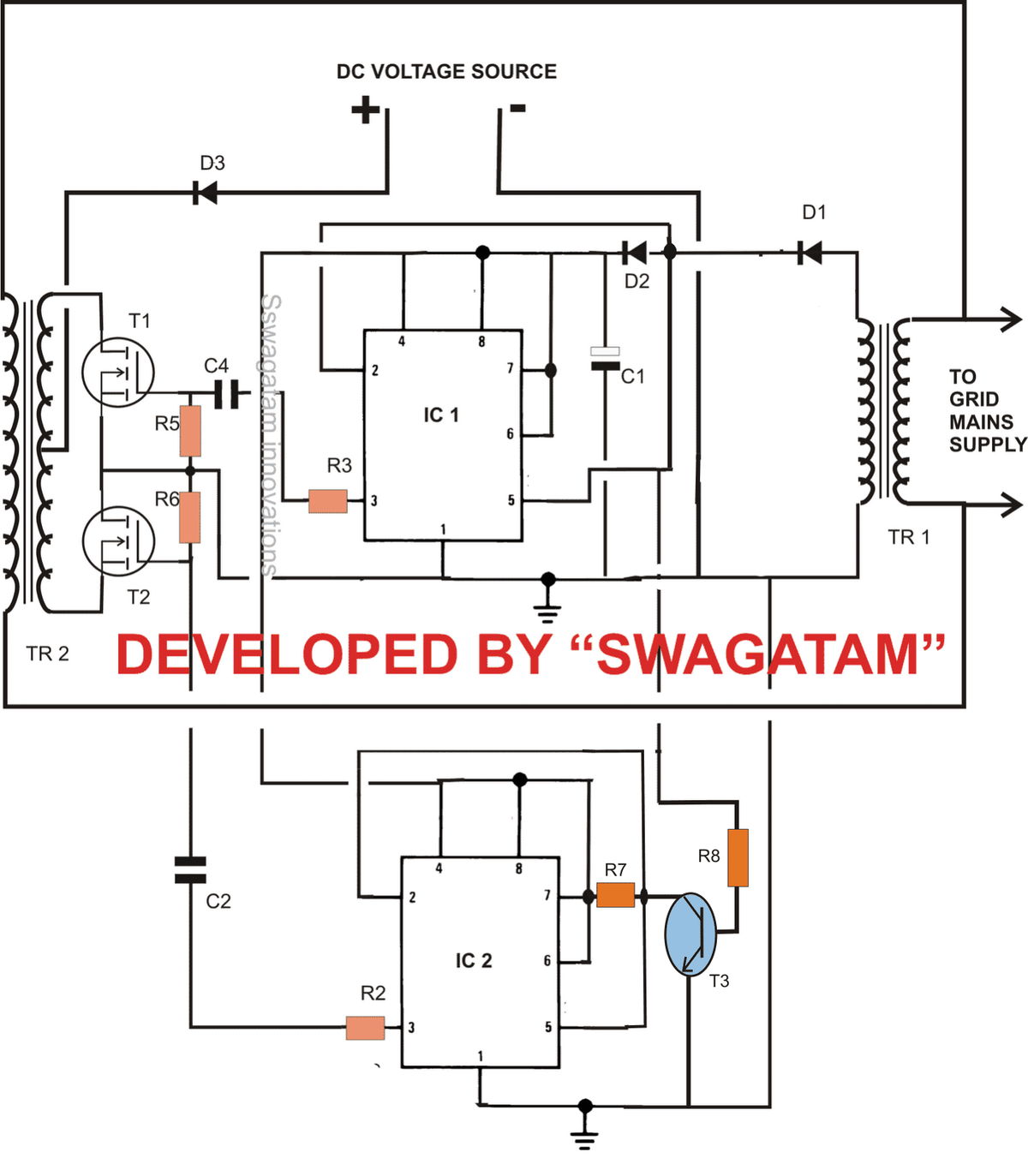
Blockdiagramm des harmonischen Oszillators
Es gibt einen Punkt in der harmonischen Bewegung, an dem das System schwingt, und die Kraft, die die Masse immer wieder an den gleichen Punkt bringt, an dem sie beginnt, wird als Rückstellkraft und der Punkt als Gleichgewichtspunkt oder mittlere Position bezeichnet. Dieser Oszillator ist auch als bekannt linearer harmonischer Oszillator . Die Energie fließt aus aktiv Komponenten zu passiven Komponenten im Oszillator.
Blockdiagramm
Das Blockschaltbild des harmonischen Oszillators besteht aus ein Verstärker und ein Feedback-Netzwerk. Der Verstärker wird verwendet, um die Signale zu verstärken, und die verstärkten Signale werden durch ein Rückkopplungsnetzwerk geleitet und erzeugen den Ausgang. Dabei ist Vi die Eingangsspannung, Vo die Ausgangsspannung und Vf die Rückkopplungsspannung.
Beispiel
Messe an einem Frühling: Die Feder liefert eine Rückstellkraft, die die Masse beschleunigt, und die Rückstellkraft wird ausgedrückt als
F = ma
Wobei 'm' die Masse und a eine Beschleunigung ist.

Masse auf einer Feder
Die Feder besteht aus einer Masse (m) und einer Kraft (F). Wenn die Kraft die Masse an einem Punkt x = 0 zieht und nur von der x - Position der Masse abhängt und die Federkonstante durch einen Buchstaben k dargestellt wird.
Arten von harmonischen Oszillatoren
Zu den Typen dieses Oszillators gehören hauptsächlich die folgenden.
Forced Harmonic Oscillator
Wenn wir die Bewegung des Systems mit äußerer Kraft beaufschlagen, spricht man von einem erzwungenen harmonischen Oszillator.
Gedämpfter harmonischer Oszillator
Dieser Oszillator ist definiert als, wenn wir eine externe Kraft auf das System ausüben, verringert sich die Bewegung des Oszillators und seine Bewegung wird als gedämpfte harmonische Bewegung bezeichnet. Es gibt drei Arten von gedämpften harmonischen Oszillatoren

Dämpfungswellenformen
Überfeuchtet
Wenn sich das System langsam in Richtung des Gleichgewichtspunkts bewegt, spricht man von einem überdämpften harmonischen Oszillator.
Unter gedämpft
Wenn sich das System schnell dem Gleichgewichtspunkt nähert, spricht man von einem überdämpften harmonischen Oszillator.
Kritisch gedämpft
Wenn sich das System so schnell wie möglich bewegt, ohne um den Gleichgewichtspunkt zu schwingen, spricht man von einem überdämpften harmonischen Oszillator.
Quantum
Es wurde von Max Born, Werner Heisenberg und Wolfgang Pauli an der Universität Göttingen erfunden. Das Wort Quantum ist das lateinische Wort und die Bedeutung von Quantum ist eine kleine Energiemenge.
Nullpunkt-Energie
Die Nullpunktsenergie wird auch als Grundzustandsenergie bezeichnet. Es ist definiert, wenn die Grundzustandsenergie immer größer als Null ist und dieses Konzept von Max Planck in Deutschland und der 1990 entwickelten Formel entdeckt wird.
Durchschnittliche Energie der gedämpften einfachen harmonischen Oszillatorgleichung
Es gibt zwei Arten von Energien: kinetische Energie und potentielle Energie. Die Summe aus kinetischer Energie und potentieller Energie ist gleich der Gesamtenergie.
E = K + U ………………. Gleichung (1)
Wobei E = Gesamtenergie
K = kinetische Energie
U = potentielle Energie
Wobei k = k = 1/2 mvzwei………… Gleichung (2)
U = 1/2 kxzwei………… Gleichung (3)

Schwingungszyklus für Durchschnittswerte
Die Durchschnittswerte der kinetischen und potentiellen Energie pro Schwingungszyklus sind gleich
Wo vzwei= vzwei(ZUzwei-xzwei) ……. Gleichung (4)
Ersetzen Sie Gleichung (4) in Gleichung (2) und Gleichung (3)
k = 1/2 m [wzwei(ZUzwei-xzwei)]
= 1/2 m [Aw cos (wt + ø0)]zwei……. Gleichung (5)
U = 1/2 kxzwei
= 1/2 k [A sin (wt + ø0)]zwei……. Gleichung (6)
Durch Ersetzen von Gleichung (5) und Gleichung (6) in Gleichung (1) wird der Gesamtenergiewert erhalten
E = 1/2 m [wzwei(ZUzwei-xzwei)] + 1/2 kxzwei
= 1/2 m wzwei-1/2 m wzweiZUzwei+ 1/2 kxzwei
= 1/2 m wzweiZUzwei+1/2 xzwei(K-mwzwei) ……. Gleichung (7)
Wo mwzwei= K. , ersetze diesen Wert in Gleichung (7)
E = 1/2 K A.zwei- 1/2 Kxzwei+ 1/2 xzwei= 1/2 K A.zwei
Gesamtenergie (E) = 1/2 K A.zwei
Die durchschnittlichen Energien für einen Zeitraum werden ausgedrückt als
ZUDurchschn= U.Durchschn= 1/2 (1/2 K A.zwei)
Harmonische Oszillatorwellenfunktion
Der Hamilton-Operator wird als Summe aus kinetischer Energie und potentieller Energie ausgedrückt und als ausgedrückt
ђ (Q) = T + V ……………… .eq (1)
Wobei ђ = Hamitonischer Operator
T = kinetische Energie
V = potentielle Energie
Um die Wellenfunktion zu erzeugen, müssen wir die Schrödinger-Gleichung kennen und die Gleichung wird ausgedrückt als
-đzwei/ 2μ * dzweiѱυ(Q) / dQzwei+ 1 / 2KQzweiѱυ(Q) = E.υѱυ(Q) …………. Gleichung (2)
Wobei Q = Länge der Normalkoordinate
Μ = effektive Masse
K = Kraftkonstante
Die Randbedingungen der Schrödinger-Gleichung sind:
Ѱ (-∞) = ø
Ѱ (+ ∞) = 0
Wir können auch die Gleichung (2) als schreiben
dzweiѱυ(Q) / dQzwei+ 2μ / đzwei(E.υ-K / 2 * Q.zwei) ѱυ(Q) = 0 ………… Gleichung (3)
Parameter, die zum Lösen einer Gleichung verwendet werden, sind
β = ђ / √μk ……… .. Gleichung (4)
dzwei/ dQzwei= 1 / βzweidzwei/ dxzwei………… .. Gleichung (5)
Ersetzen Sie Gleichung (4) und Gleichung (5) durch Gleichung (3), dann wird die Differentialgleichung für diesen Oszillator
dzweiѱυ(Q) / dxzwei+ (2 μbzweiE.υ/ đzwei- xzwei) ѱυ(x) = 0 ……… .. Gleichung (6)
Der allgemeine Ausdruck für Potenzreihen lautet
ΣC¬nx2 …………. Gleichung (7)
Eine Exponentialfunktion wird ausgedrückt als
exp (-xzwei/ 2) ………… Gleichung (8)
Gleichung (7) wird mit Gleichung (8) multipliziert.
ѱυ (x) = ΣC¬nx2exp (-x2 / 2) …………… ..eq (9)
Hermite-Polynome werden unter Verwendung der folgenden Gleichung erhalten
ђυ(x) = (-1)υ* exp (xzwei) d / dxυ* exp (-xzwei) …………… .. Gleichung (10)
Die Normalisierungskonstante wird ausgedrückt als
N.υ= (1/2υυ! √Π)1/2…………… .eq (11)
Das einfache harmonische Oszillatorlösung wird ausgedrückt als
Ѱυ(x) = N.υH.υ(und) e-x2 / 2……………… Gleichung (12)
Wo N.υist die Normalisierungskonstante
H. υ ist der Einsiedler
ist -x2 / zweiist der Gaußsche
Eine Gleichung (12) ist die Wellenfunktion des harmonischen Oszillators.
Diese Tabelle zeigt den ersten Term Hermite-Polynome für die Zustände mit der niedrigsten Energie
| υ | 0 | 1 | zwei | 3 |
H.υ(Y) | 1 | 2y | 4yzwei-zwei | 8y3-12y |
Die Wellenfunktionen der einfacher harmonischer Oszillator Graph Für vier Zustände mit der niedrigsten Energie sind die folgenden Abbildungen dargestellt.

Wellenfunktionen des harmonischen Oszillators
Die Wahrscheinlichkeitsdichten dieses Oszillators für die vier Zustände mit der niedrigsten Energie sind in den folgenden Abbildungen dargestellt.

Wahrscheinlichkeitsdichten von Wellenformen
Anwendungen
Die sharmonischen Oszillator implementierenAnwendungen umfassen hauptsächlich die folgenden
- Audio- und Videosysteme
- Radio und andere Kommunikationsgeräte
- Wechselrichter , Alarme
- Summer
- Dekorative Lichter
Vorteile
Das Vorteile des harmonischen Oszillators sind
- Billig
- Hochfrequenzerzeugung
- Hohe Effizienz
- Billig
- tragbar
- Wirtschaftlich
Beispiele
Das Beispiel dieses Oszillators umfasst Folgendes.
- Musikinstrumente
- Einfaches Pendel
- Massefedersystem
- Schwingen
- Die Bewegung der Zeiger der Uhr
- Die Bewegung der Räder von Auto, LKW, Bussen usw.
Es ist eine Art von Bewegung, die wir täglich beobachten können. Harmonisch Oszillator Wellenfunktion unter Verwendung von Schrödinger und Gleichungen des harmonischen Oszillators werden abgeleitet. Hier ist eine Frage, welche Art von Bewegung durch Bungee-Jumping ausgeführt wird?